Here's an equivalent circuit for a raw dynamic driver.  It doubles as one for a sealed (or enclosed driver) where “Rg” is speaker cable impedance & cross-over resistance & amplifier's output impedance.  For what it's worth, most people ignore “Rms”.

The magnitude of the impedance for real world driver is plotted below.  The low frequency spike is modeled by the “Ces”; “Res”; “Les” section of the circuit while the high frequency slope is the responsibility of “Le” (voice coil inductance).

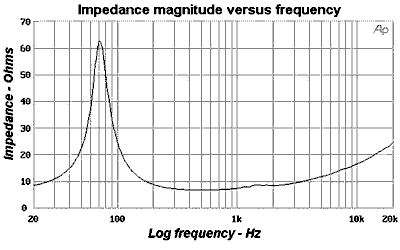
From this we can glean Thiele-Small parameters, if not supplied.  We will need the maximum impedance ( Zmax ≈ 63Ω ) atop the resonance spike & the minimum ( Zmin ≈ 7Ω ) in the well following.  Now, we calculate the “R1” value which is the log mean value ( R1 = Sqrt[Zmax×Zmin] ≈ 21Ω ).  Now we look for “f1” & “f2”, which are frequencies about the spike where the impedance is “R1” (IE: 48Hz & 105Hz respectively).  In lieu of “Re”, we will ignore “Rms” & subsequently equate “Re” with “Zmin”, because Zmin = Re + Rms.

R_es = Z_max - R_e
( 56Ω )

C_es = Sqrt[Z_max/R_e]/( 2×p×(f₂ - f₁)×R_es)
( 149.6 µF )

L_es = (f₂ - f₁)×R_es×Sqrt[R_e/Z_max]/( 2×p×f₁×f₂)
( 33.6 mH )

Now that we modeled the difficult part, let's find “Le”.  Let's take a read of 17Ω @ 10kHz where the inductance is significant.

L_e = Sqrt[ Z_10kHz² - Z_min² ] / ( 2 × p × 10000Hz )
( 0.247 mH )

Below is a reconstruction of the impedance curve in yellow.

Here's the actual published data for the same driver.

Re	6 Ω
Le	0.24 mH
Qes	0.34
Qms	4.27
fs	70.7 Hz

So when given this data:

R_es = R_e × Q_ms / Q_es
( 75.35Ω )

C_es = Q_es /( 2 × p × f_s × R_e )
( 127.56 µF )

L_es = R_e /( 2 × p × f_s × Q_es)
( 39.73 mH )

Here's the actual published values:

Ces	125.0 µF
Res	77.0 Ω
Les	40.6 mH

Conjugate Filters

Now you know how to derive these values & you wonder why.  Well, we can obliterate the spike by using a simple L;R;C conjugate filter.  This is a series configuration whose entirety is wired in parallel across a dynamic driver's terminals.  Therefore, the low frequencies look like a resistor as depicted by the red line in the above impedance graph.

0—————[ Ln ]—————[ Rn ]—————[ Cn ]—————0

L_n = C_es × R_e²

R_n = R_e ×( R_e + R_es )/ R_es

C_n = L_es / R_e²

Zobel Circuit

Similarly, a Zobel circuit nullifies the voice coil inductance.  This R;C circuit is also wired across the driver's terminals.  A graphed blue line illustrates what a Zobel does.

0———————[ Rz ]————————[ Cz ]———————0

R_z = R_e + R_ms

C_z = L_e/R_z²

So what was this about?  Well, if you want a cross-over to work, it depends on your driver resembling a resistor.

Acoustic Response

Is that the only reason?  No.  Acoustics response is proportional to the voltage drop across “Rms”.

In this case, we have the published measured data:

What happens if all you have the is the impedance graph instead?  Well, a well known low frequency response curve is based on “Qh” & “fh” which is equivalent to “Qtc” & “fb” (the enclosed version of Qts & fs), respectively.

f_s = Sqrt[ f₁ × f₂ ]
( 71 Hz )

R₀ = Z_max / Z_min
( 9 )

Q_ms = f_s × Sqrt[R₀] /( f₂ - f₁ )
( 3.74 )

Q_es = Q_ms /( R₀ - 1 )
( 0.467 )

Q_ts = Q_ms × Q_es /( Q_es + Q_ms )
( 0.415 )

Here's the actual published values:

fs	70.7 Hz
Qms	4.27
Qes	0.34
Qts	0.32
SPL	90.9 dB/m/W

For those that understand complex equations ... the transfer fuction is :

(f/f_h)² / { (f/f_h)² - Sqrt[-1]×f/(f_h×Q_h) - 1 }

Associated group delay plotted in equivalent phase angle:

The equivalent electric circuit for a ported enclosure schematic is:

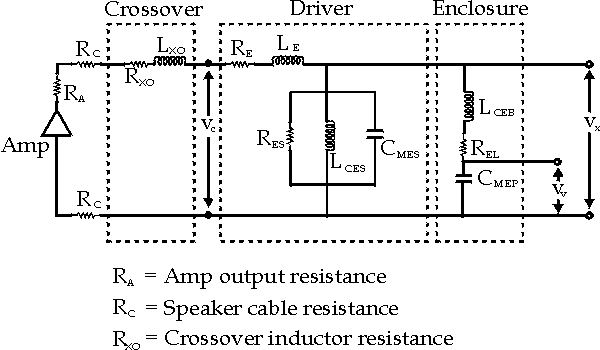
further elaboration