How Maggies work, Part IV
Now letís examine how they propel sound. Namely dispersion. Conventional speaker drivers function like point-sources. Thatís when the driver dome or cone has a diameter smaller than the wavelength of sound it reproduces. Thatís why you can stand completely to one side of an 8" diameter cone woofer & still hear bass frequencies like you were in front, but lose midrange frequencies. An 8" wavelength corresponds to 1.7kHz. This is the delineation point for the 8" woofer.
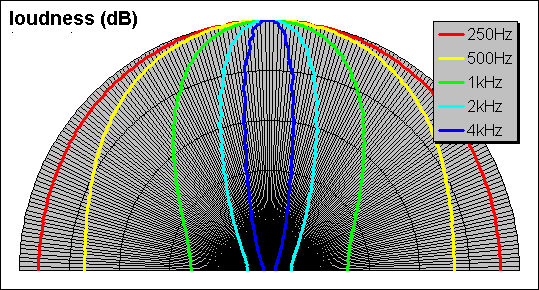
However, loudspeaker driver manufacturers usually plot it like ...
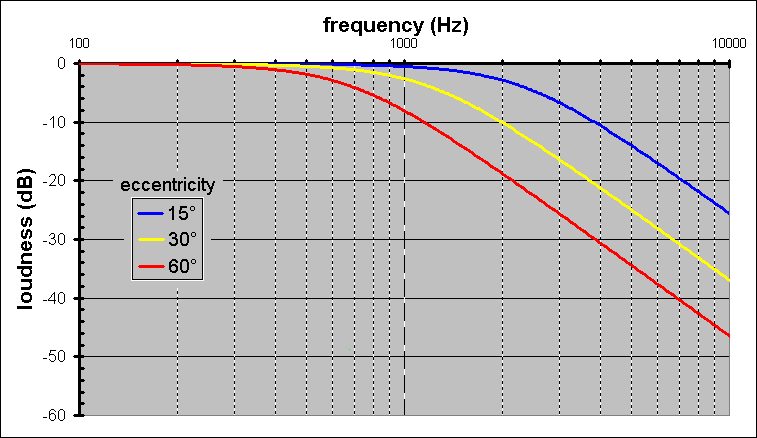
It is said that the higher frequencies beam (like headlights) instead of disperse waves like ripples in a pool at the lower frequencies. Now suppose the loudspeaker was a 3-way that had a dedicated 4" midrange driver. Thus, the woofer never operated in its beamed frequency range. Thus, it disperses all frequencies it was asked to reproduce as if from a comparatively small driver, or point. Thatís why we call it a point-source.
This can be actively modified through diaphragm shape. This is why tweeter discs are predominantly domed. Letís take a common 1" dome. If the tweeter were flat, then frequencies above 14kHz would be attenuated if not directly off axis to it. What a bummer. Talk about an infinitesimal sweet spot! However, sound waves prefer to propagate normal (perpendicular) to the diaphragm. Thus, once the diaphragm is curved, it actively pushes sound waves eccentrically to aide dispersion.
Now, letís examine planars. Suppose we have a conventional ribbon thatís ½" wide by 5' tall & its acoustical frequency response operates from 1kHz to 30kHz. The ½" width means it will disperse laterally any wavelengths larger than ½" (IE: frequencies it can reproduce below 27kHz) if not physically obstructed by horn loading, or magnets, or mounting. However, the 5' height diaphragm length limits vertical dispersion. Thus, it will beam frequencies above 230Hz. In order words, for all intense purposes the ribbon disperses only laterally throughout its acoustic operational band. This behavior defines a line-source & given this example you can see how it got its name.
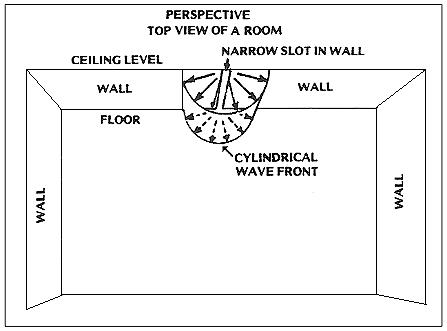
So, is there a difference worth mentioning? Yes. Letís recall that sound waves contain energy. Letís follow a sound wave from a comparatively small diaphragm. The diaphragm excurts to compress the air in front of it & then propel that compression wave radially outward to every growing wavefront.
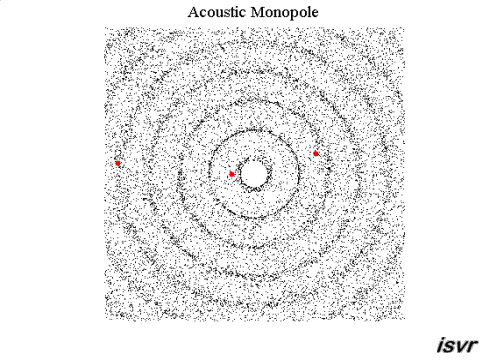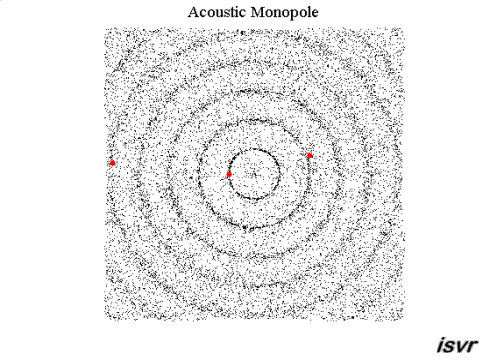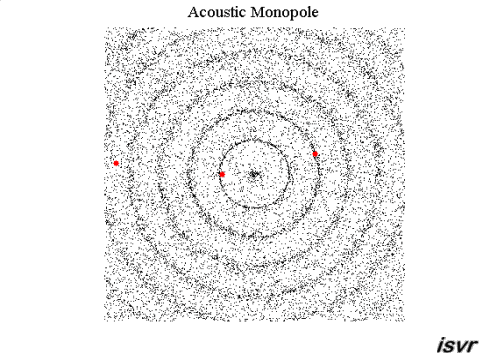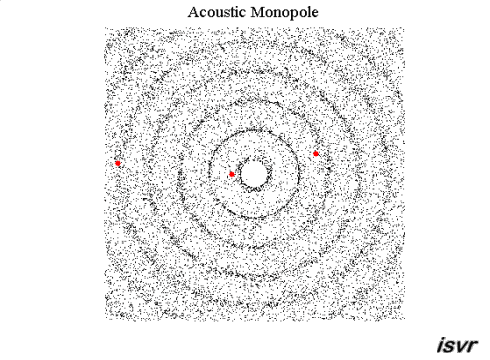
As the wave expands its pressure dissipates as its energy is equi-distributed. How now becomes important. Its thickness is fixed by the wavelength along with its frequency. So, the wavefront area defines the phenomena. A line-source disperses in one-dimension (usually laterally). The compression wave expands from the line-source as a propagating cylindrical shell. Thus, the energy density is a function of cylindrical area. Thatís why we perceive the loudness to drop as a reciprocal linear function of distance, or 1/R.
By the same reasoning, a point-source propagates a spherical sound wave. Itís two-dimensional, vertical & lateral. So, itís loudness drops as a square of a line-source, or 1/R≤.
So, if we compared two loudspeakers that are identically efficient 90dB/W at 1 m. The loudness changes with distance like ...
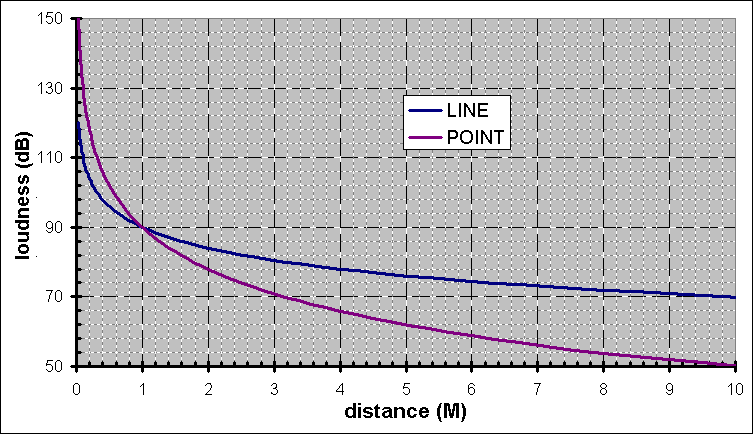
This reduced dispersion is why line-sources sound louder at a distance. It is also why first reflections off side walls are more important with line-sources as the longer paths are proportionately louder contributions. Finally, it makes means hybrid loudspeakers are prone to change tone at different listening distances.
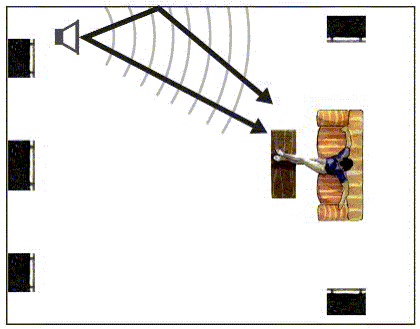
EG: Suppose we were comparing two loudspeakers operating at equivalent loudness 9'(~2¾M) away & the reflection off from the sidewall travels a 15'(~4½M) path. We see that (assuming an acoustically-reflective wall & ideal dispersion) the reflected sound is 8.9dB down from a point-source versus 4.4dB from a line-source.
Hereís where I add a footnote regarding some electrostatic loudspeakers. Conventional flat electrostats behave like planar-sources. They are tall & wide enough not to disperse instead they project a large swath. Thus, they maintain their loudness with distance until long bass wavelengths that still do disperse. Couple that with a dipolar configuration & weíre talking audible bass attenuation.
Some manufacturers curve their membranes into a partial cylinder; either directly like a Maggie center channel and a Martin Logan CSLs or facetted like Sound-Lab ESLs. This actively propagates a limited cylindrical wave to mimic a line-source.
How Maggies work, Part V
Now letís talk about interference patterns of a dipole that alters dispersion patterns. Pictured below is radiation pattern of a dipole firing sideways. Which way doesnít matter.

The left waves are equal & opposite of those on the right. They cancel each other where these contradictory waves are superimposed off-axis (top & bottom). This is called destructive interference. It creates a classic figure 8 pattern.
This is different from a bipole in that both sides of the speaker are in phase. Therefore their off-axis response constructively reinforce each other. Thatís why theyíre renown for their dispersion & an ideal bipolar speaker resembles our previous picture.

Now letís examine back-wall reflections. Pictured below is a loudspeaker positioned 3' distance to a highly-reflective back-wall. We are comparing dipolar speakers with bipolars (where the back-wave & front-wave are synchronized much like the single-source pictured above). We witness what happens when the back-wave is initiated off the rear of the speaker at time T1 propagates rearward & reflects off the back-wall & transverses back to the speaker where it recombines with the new front-wave just being initiated at time T2. This temporal discrepancy accounts means that at some frequencies the two waves destroy each other & other times it reinforces ...
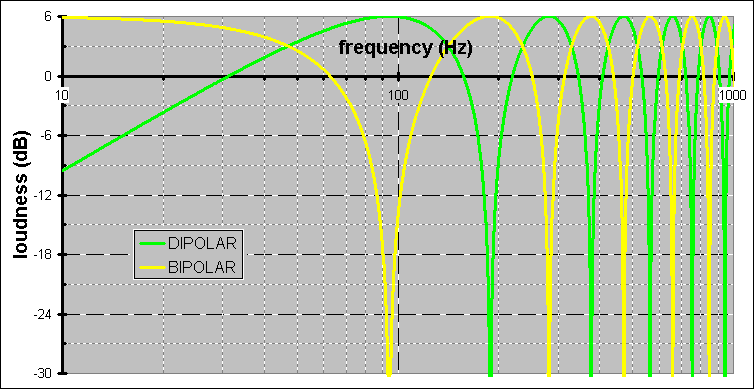
This effect is called comb filtering, which is why many dipolar fans treat the back-wall with absorbent material. It absorbs everything but long bass wavelengths. Thatís how comb-filtering is prevented. Also, de-paralleling the planar form the back-wall like toeing-in helps too.
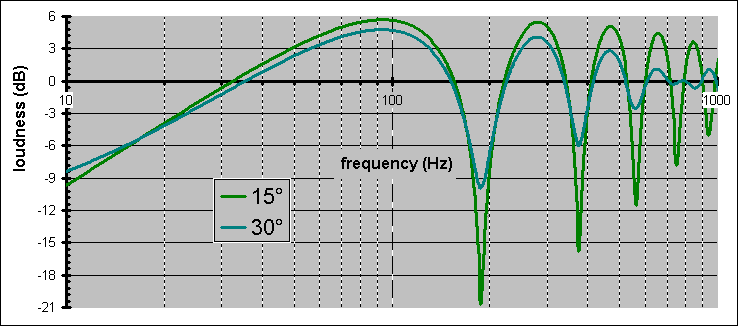
Now, picture two adjacent drivers operating synchronously. This often happens in an acoustic Linkwitz-Riley crossover at the crossover frequencies. Hereís why they should be no more than a wavelength apart. Demonstrated here is two wavelengths. The eccentricity position specific response is called lobing for constructive reinforcement & nulls for destructive interference.

